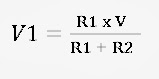Series Resistors and Voltage Division, Parallel Resistors Current Division

Series Resistors

                      Resistors are connected in series when they are chained together in a single line. all the current flowing from one resistor will also pass the other resistors and has no other way to go because they have only path.

                   

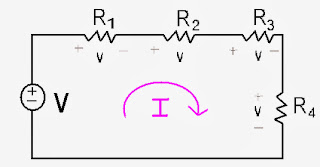
In this circuit we have four resistors and one voltage source. All we need to do is to follow the following formulas:

Resistance: R_eq  = R₁ + R₂  +  R₃ +_{………………}R_n
Voltage:     V_eq = V₁ + V₂ + V₃+...…...V_n
Current:        I_eq  =  I₁ = I₂ = I₃ = …….....…..In 

Voltage Division

              

In solving by voltage division we must remember that the circuit contains two resistors and one voltage source connected in series.

voltage division formula:

  

V1 is voltage from R1 as well as V2. V in the numerator is the voltage source.

                                 

 Parallel Resistors

A resistor is in parallel to another resistor  if and only if they share common terminals. In our circuit Both the branches touch each other's endpoint.

 formula:

                

Current Division

   

In solving current division note that you should have two paralleled resistors and one current source (see illustration above) so that we can apply the given formula.

Kirchhoff"s Law

Before we discuss this topic we must first understand some basic concepts of network topology.

in a circuit there is what we called the BRANCHES, NODES and LOOPS.

branch- represents a single element such as a voltage source or a resistor. (boxed)

node- is the point of connection between two or more branches. (circled)

loop-is any closed path in a current. (directional arrow)

In our circuit, we have 4 branches, namely the voltage source current source and two resistors, three nodes indicated by a dot in a circuit, and two loops. If you wonder why there are only three nodes, it is because the two nodes constitute a single node.

a network with branches (b), nodes (n), and loops (l) will satisfy the fundamental theorem of network topology.

                                                     

Now, let's name the branches that we will use for this whole discussion.

Independent voltage source                                                      dependent voltage source

                                                                         

   

Independent current source                                                         dependent current source

                                                                                

resistors

                      

                                  

             

                                          

Kirchhoff's Current Law or KCL

                                                   

                                                    current entering    =     current leaving

KCL states that the algebraic sum of the currents in all the branches that converge in a common node is equal to zero.

I₁ = I₂ + I₃

I₁ + I₄  = I₂ + I₃ + I₅

Kirchhoff's Voltage Law or KVL

KVL

states that the algebraic sum of the voltages between successive nodes in a closed path in a circuit is equal to zero. We assume that the Resistor has its polarity and our loop is in clockwise direction.

we will use V = I x R in every resistor cause KVL talks about voltage. every loop has one equation so in this circuit we have 1 equations. For resistors we have unknown polarities so lets assume that all current from the resistors are positive.

equation:     R₁ x I₁ + R₂ x I1 + V = O , 

V is positive because in my convention I get the first sign as where the directional arrow enters first so that my equation contains less negative signs.

           

you may use also this equation;  -(R₁ x I₁ ) -(R₂ x I1) - V = O as long as your current from all resistors are set to negative and V must read the last sign but for the whole discussion we will use the first equation's convention.

1st eq.   R₁ x I₁ + R₂ x (I₁-I₂) + V = O

(I₁-I₂) came from resistor 2 because the two current shares one resistor at a time.

2nd eq.   R₃ x I₂ + R₂ x (I_2- I₁) - V = O

(I₂ - I₁) still came from resistor 2 previously I₁ comes first because we are in loop 1 but this time I₂ comes first because we are in loop 2.